
Prof. Thierry Blu
FIEEE, FHKIE
News
Fractional splines
Properties
The fractional splines are an extension of the polynomial splines for all fractional degrees α > -1 (α > -1/2 for square integrable functions) and real number τ ("shift"). The Fourier transform of the B(asic) fractional splines is
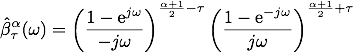
Their basic constituents are piecewise power functions of degree α (except for degenerate cases). One constructs the corresponding B-splines through a localization process similar to the classical one, replacing finite differences by fractional differences. The fractional B-splines share virtually all the properties of the classical B-splines, including the two-scale relation, and can therefore be used to define new wavelet bases with a continuously-varying order parameter. They only lack positivity and compact support.
The fractional splines have the following remarkable properties:
-
Generalization: for α integer, they are equivalent to the classical polynomial splines. As can be seen in these animations
the fractional B-splines interpolate the polynomial ones in very much the same way as the gamma function interpolates the factorials (in red, the usual B-splines). - Shifting: The τ parameter essentially represents a shift of the basis function, at least for a degree α that is large enough as can be seen in these animations
- Regularity: the fractional splines are α-Hölder continuous; their critical Sobolev exponent is α + 1/2.
- Decay: the fractional B-splines decay at least like |x|-α-2; they are compactly supported for α integer and (α odd in the symmetric case).
- Order of approximation: the fractional splines have a fractional order of approximation α + 1; a property that has not been encountered before in wavelet theory.
- Vanishing moments: the fractional spline wavelets have ceil(α)+1 vanishing moments, while the fractional B-splines reproduce the polynomials of degree ceil(α).
- Fractional derivatives: simple formulæ are available for obtaining the fractional derivatives of B-splines. In addition, fractional spline wavelets essentially behave like fractional derivative operators.
- Stretching the bounds of wavelet theory: for -1/2 < α < 0, the fractional B-splines don't have the standard regularity factor (1+z). Yet, they yield perfectly valid wavelet bases with some rather strange characteristics (order of approximation lesser than 1, singularities at the integers, etc...).
References
| [1] Unser, M. & Blu, T.,"Fractional Splines and Wavelets", SIAM Review, Vol. 42 (1), pp. 43-67, March 2000. |
| [2] Blu, T. & Unser, M.,"The Fractional Spline Wavelet Transform: Definition and Implementation", Proceedings of the Twenty-Fifth IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP'00), Istanbul, Turkey, Vol. {I}, pp. 512-515, June 5--9, 2000. |
| [3] Blu, T. & Unser, M.,"A Complete Family of Scaling Functions: The ($alpha,tau$)-Fractional Splines", Proceedings of the Twenty-Eighth IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP'03), Hong Kong, China, Vol. {VI}, pp. 421-424, April 6--10, 2003. |
Matlab Software
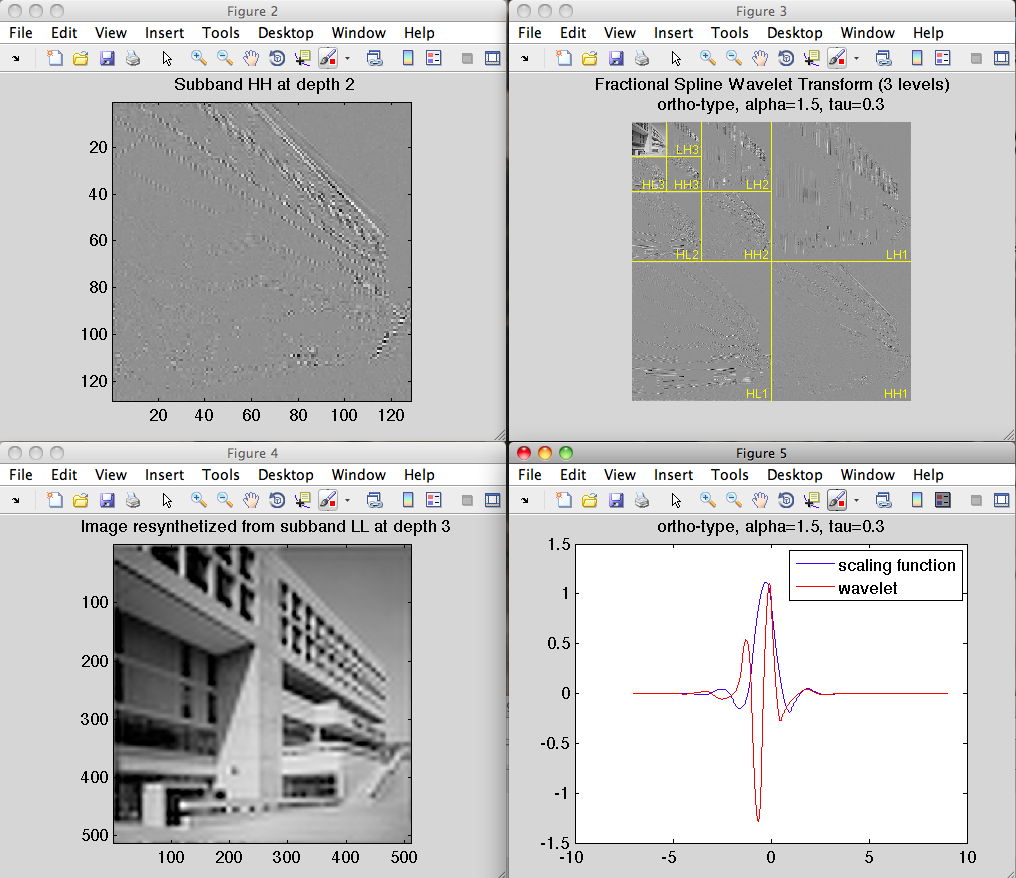
Despite their non-conventional properties and lack of compact support, the fractional spline wavelets are perfectly implementable. The Matlab code available here is a demo of the fractional spline wavelet decomposition algorithm described in the above papers. Download the zip archive. To understand how to use these files, please read the file README.txt or the online help in the routines.You may also wish to try the java demo of the Biomedical Imaging Group at EPFL.
demo2D snapshot
Conditions of use
—
You are free to use this software for research purposes, but you should not
redistribute it without our consent. In addition, we expect you to include an
adequate citation and acknowledgment whenever you present or publish results that are based on it.
demo2D snapshot