Prof. Thierry Blu
FIEEE, FHKIE
News
Fast and Accurate 3D PSF Computation for Fluorescence Microscopy
Jizhou Li, Feng Xue and Thierry Blu
Outline
The point-spread function (PSF) of a microscope describes the response of this imaging system to a point source or object. A realistic and accurately calculated PSF model can significantly improve the performance of deconvolution microscopy and also the localization accuracy in single-molecule microscopy.
Among microscopy PSF models, Gibson-Lanni's (JOSA-A, 9, 154–166, 1992) is particularly useful since it involves explicitly design and experimental physical parameters. It is based on Kirchhoff's diffraction integral formula:
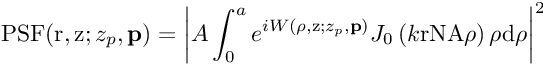
where the phase term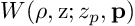 
has an explicit expression involving several physical parameters, and 
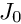denotes the Bessel function of the first kind of order zero. k is the wave number of the fluorescent light and NA the numerical aperture of the microscope.
Our approach is based on two ideas: first, express (approximate, actually) the function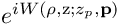 
as a linear combination of rescaled Bessel functions,
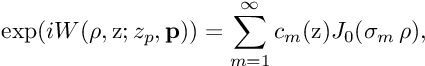where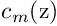 
are complex-valued coefficients (to be determined by fitting), and 
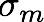are adequately chosen scaling factors; second, compute exactly Kirchhoff's integral by using the following antiderivative (a and b arbitrary):
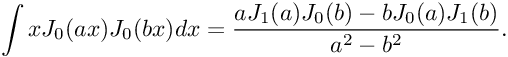
Advantages of our algorithm:
- Two orders of magnitude faster than the quadrature approach (e.g., see PSF Generator) at same accuracy.
- Can be extended to other microscopy PSF models.
Reference
| Li, J., Xue, F. & Blu, T.,"Fast and Accurate 3D PSF Computation for Fluorescence Microscopy", Journal of the Optical Society of America A, Vol. 34 (6), pp. 1029-1034, June 2017 (Top downloaded article in Oct 2017). |
Matlab Software
The Matlab code available here (220KB) is a demo that allows to generate and visualize 3D microscopy PSF based on the Gibson-Lanni model. To understand how to use these files, please read the file README.txt to understand how to start the demo.Demo snapshot
